Funkcje
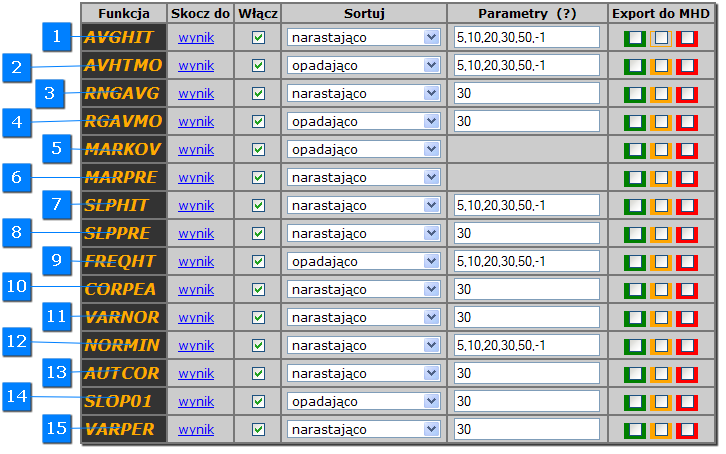

 funkcja AVGHIT funkcja AVGHIT

Funkcja AVGHIT oblicza średnią odstępów dla określonej na liście (parametrów) trafień wstecz czyli oblicza średnią oczekiwań z n trafień wstecz. Np jeżeli zestaw lub liczba trafiła 2-krotnie a jej wielkość odstępów 8 i 4 losowania to średnia wynosi 6 odstępów.
|
|
•dogóry
|
 Funkcja AVHTMO Funkcja AVHTMO

Funkcja AVHTMO oblicza różnicę ostatniego odstępu i średnią odstępów z listy (parametr) trafień wstecz czyli oblicza średnią oczekiwań z n trafień wstecz. Oblicza więc ile aktualnie liczba czy zbiór oczekuje dłużej niż wynika to z średniej odstępów z n trafień wstecz. Wartość dodatnia oznacza oczekiwanie dłuższe niż średnia ostatnich wystąpień. Przykład: czyli wartość funkcji AVGHIT minus OSTATNI_ODSTĘP : a więc, jeżeli zestaw lub liczba trafiła 2-krotnie a jej wielkość odstępów 8 i 4 losowania to średnia to 6 odstępów. Więc wartość funkcji 6 - 8 = -2. Liczba czy zbiór oczekuje dłużej niż wynika to ze średniej trafień w badanym okresie 2 trafień.
|
|
•dogóry
»Dalej
|
 Funkcja RNGAVG Funkcja RNGAVG

Funkcja RNGAVG działa jak funkcja AVGHIT, z tą różnicą że zakres średniej oczekiwań obliczony jest z listy losowań a nie z listy kolejnych trafień. Przykład: W 30 losowaniach (parametr) wylosowano liczbę 6 razy wiec średnia wyniesie 5. Pięć jest wartością funkcji.
|
|
•dogóry
|
 Funkcja RGAVMO Funkcja RGAVMO

Funkcja RGAVMO działa jak funkcja AVHTMO, z tą różnicą że zakres średniej oczekiwań obliczony jest z listy (n losowań) a nie z listy kolejnych trafień.
|
|
•dogóry
|
 Funkcja MARKOV Funkcja MARKOV

Funkcja MARKOV oblicza matryce prawdopodobieństwa Markowa. Dla wszystkich trafień w bazie losowań budowana jest tablica prawdopodobieństw przejść odstęp przed trafieniem -> trafienie. I na tej podstawie obliczany jest wynik określający prawdopodobieństwo trafienia w następnym losowaniu. Prawdopodobieństwo bliskie jedności oznacza zdarzenie prawie pewne, bliskie zeru prawdopodobieństwo znikome.
|
|
•dogóry
|
 Funkcja MARPRE Funkcja MARPRE

Funkcja MARPRE działa jak funkcja MARKOV, z tą różnicą że na podstawie tablicy prawdopodobieństw przejść ostatni odstęp-> trafienie, wybierany jest z tablicy najbardziej prawdopodobny następny odstęp do następnego wylosowania. Odstęp równy 0 (zero) oznacza że funkcja "przewiduje" wystąpienie liczby w następnym losowaniu.
|
|
•dogóry
|
 Funkcja SLPHIT Funkcja SLPHIT

Funkcja SLPHIT oblicza TREND z kolejnych odstępów o długości wektora branego z listy (n losowań) wstecz od ostatniego. W obliczeniach zmienną zależną (y) są kolejne wartości odstępów o długości wektora zadanej parametrem z listy a zmienną zależną (x) są ciągi kolejnych losowań narastająco z kolejnym losowaniem.
Dlatego trendy dodatnie wskazują że w zadanym parametrem okresie trafienia występowały na początku okresu, wyniki bliskie zeru wskazują ze w zadanym okresie trafienia są regularne, wartości ujemne to trafienia na końcu badanego okresu. Trend jest "odwrotny" ponieważ analizie poddawany jest przebieg (piły) odstępów, zero to trafienie a odstępy kolejno rosną co losowanie gdy trafienia nie występuje. Stąd nazwa przebieg przypominający zęby piły.
|
|
•dogóry
|
 Funkcja SLPPRE Funkcja SLPPRE

Funkcja SLPPRE działa jak funkcja SLPHIT, z tym że na podstawie wyliczonego trendu wyliczany jest następny spodziewany odstęp liczby czy odstęp badanego zbioru.
|
|
•dogóry
|
 Funkcja FREQHT Funkcja FREQHT

Funkcja FREQHT oblicza częstość trafień w zadanym parametrem zakresie losowań wstecz. * Parametr o wartości -1 oznacza wszystkie losowania.
|
|
•dogóry
|
 Funkcja CORPEA Funkcja CORPEA

Funkcja CORPEA oblicza współczynnik korelacji liniowej Pearsona, przebiegiem porównywanym (korelowanym) jest przebieg (wzorcowy) wyliczony ze statystycznej normy trafień. Np dla parametru =5 przebiegiem badanym jest przebieg ostatnich pieciu odstepów np: 6,8,4,3,6 a przebiegiem wzorcowym dla MULTI(KENO) 1/80 jest przebieg (4,4,4,4,4) ponieważ każda liczba "powinna" wystąpić co 4 losowania.
|
|
•dogóry
|
 Funkcja VARNOR Funkcja VARNOR

Funkcja VARNOR oblicza współczynnik wariancji z listy ostatnich losowań wstecz. Współczynnik ten określa równomierność zbioru. Wartości współczynnika zbliżone do zera oznaczają równomierność trafień w zadanym listą okresie losowań.
|
<|
•dogóry
|
 Funkcja NORMIN Funkcja NORMIN

Funkcja NORMIN oblicza częstość trafień w zadanej listą ilości losowań wstecz oraz odejmuje od tej wartości statystyczną normę wynikającą z rachunku prawdopodobieństwa.
Różnica ta wskazuje czy liczba (wypełnia) normę wynikającą z rachunku statystycznego. Wartości dodatnie mówią że liczba występuje w zadanym okresie częściej a ujemne że rzadziej niż wynikało by to z rachunku prawdopodobieństwa. Funkcja ta przypomina tzw piramidkę liczb. Uwaga: dla zbiorów należy dobrze zadać parametry zakresów na jakich ma funkcja obliczyć normę, ponieważ np gdy badamy zbiory np 6 liczbowe i badamy w nich trafienia 6-ek to normą będzie np dla DL jedno trafienie na 14 mln losowań, w bazie nie ma tylu losowań wówczas wyniki funkcji nic nam nie powiedzą o wielkości aktualnej normy. Wielkość normy można sprawdzić w kalkulatorze szans: przykład mamy zbiór 10 liczb w Expres Lotku 42 liczby 5 losowanych a w bazie losowań ok 800 losowań. W kalkulatorze szans wybieramy szansa liczb = 5 (badamy trafienia 5 ek), przy typowaniu = 10 (nasze zbiory mają po 10 liczb), z wylosowanych = 5 (losowane jest 5 liczb), wszystkich liczb = 42 ( w ex jest 42 liczb) wynikiem jest 3375.66 więc jedno trafienie przypada na 3375 losowań. Więc nie ma praktycznie szans aby w 800 losowaniach określić normę trafień. Dla zbiorów 10 liczbowych w ex najwyższym parametrem badania trafień jest badanie trafień 4 ze zbioru 10 (co 126 losowań).
|
|
•dogóry
|
 Funkcja AUTCOR Funkcja AUTCOR

Funkcja AUTCOR oblicza współczynnik autkorelacji dla odstępów, określa on jak skorelowany jest zbiór w stosunku do zbioru cofnietego o jeden okres.
|
|
•dogóry
|
 Funkcja SLOP01 Funkcja SLOP01

Funkcja SLOP01 oblicza trend z kolejnych trafień, w funkcji w odróżnieniu od trendy obliczanego w funkcji SLPHIT nie są brane odstępy ale trafienia przy czym trafienie to jedynka, brak trafień to zero. Czyli tu wartości większe wskazują trend dodatni czyli prawdopodobne przyszłe trafienie.
|
|
•dogóry
|
 Funkcja VARPER Funkcja VARPER

Funkcja VARPER wariancji (równomierności trafień) w odróżnieniu od funkcji VARNOR robi to na zbiorach zero jedynkowych trafienie to jedynka, brak trafień to zero.
|

Funkcja PNNNET oparta na sieci (predykcji PNN). Jako zestaw treningowy wybierane są szeregi kolejnych odstepów liczb wstecz od losowania zaznaczonego jako ostatnie. Dla przykładu dla zakresu 4 bedą to przebiegi:
Np liczba miała odstępy :
5 0 1 2 3 4 5 0
To zestaw treningowy dla zakresu 4 bedzie miał postać :
1 5 0 1 2
1 0 1 2 3
1 1 2 3 4
0 2 3 4 5
W zestawie uczącym pierwsza linia oznacza odpowiedż
nastepującą po każdym szeregu czasowym przy czym nastepny
odstęp nie wylosowany a więc wiekszy od zera oznaczamy
w odpowiedzi jedynką a wylosowanie liczby oznaczamy zerem.
Tak wiec sieć podejmuje decyzje czy liczba bedzie wylosowana
lub nie bedzie wylosowana. Dlatego odpowiedziami funkcji są wartości
zero lub jeden. W przykładzie tak sa przesunięte wartosci odstępów
aby pokazać jak szeregi odstepów są brane do nauczania.
Dla linii pierwszej szereg 1 .... 5 0 1 2
oznacza ze w nastepnym okresie liczba nie była wylosowana (1)
a miała kolejne odstępy 5 0 1 2. Parametrem funkcji jest wartość
(4), poniewaz są analizowane 4 losowania wstecz.
|

Funkcja PNNSPC oparta na sieci (predykcji PNN). Jako zestaw treningowy wybierane są szeregi kolejnych odstepów liczb wstecz od losowania zaznaczonego jako ostatnie. Dla przykładu dla parametru funkcji = 4 bedą to przebiegi:
Działa analogicznie jak funkcja PNNNET lecz odpowiedzią
zestawu nauczania jest bezposrednio nastepny offset
Np liczba miała odstępy :
5 0 1 2 3 4 5 0
To zestaw treningowy dla zakresu 4 bedzie miał postać :
6 5 0 1 2
5 0 1 2 3
0 1 2 3 4
1 2 3 4 5
Tak wiec sieć podejmuje decyzję: jaki odstęp "powinien" wystapic po
danym szeregu odtepów. Dlatego odpowiedziami funkcji są wartości
nastepnego przewidywanego odstepu.
W przykładzie tak sa przesunięte wartosci odstępów
aby pokazać jak szeregi odstepów są brane do nauczania.
Dla linii pierwszej szereg 6 .... 5 0 1 2
oznacza ze w nastepnym okresie liczba nie była wylosowana (miała odstęp=6)
a w poprzednich losowaniach miała kolejne odstępy 5 0 1 2.
Parametrem funkcji jest wartość (4), poniewaz są analizowane 4
losowania wstecz.
|

Funkcja PNNETA oparta na sieci (predykcji PNN). Jako zestaw treningowy wybierane są szeregi kolejnych odstepów liczb wstecz od losowania zaznaczonego jako ostatnie. Dla przykładu dla parametru funkcji = 3 bedą to przebiegi:
Działa analogicznie jak funkcja PNNNET lecz jako kolejne odstępy
są brane odstepy przed wylosowaniem. Np liczba x była wylosowana
w poprzednich okresach po odstępach 6,8, 11
Czyli odpowiedzią będzie 0 jeżeli po takiej serii była wylosowana
i 1 jeżeli po takiej serii nie była losowana.
|

Funkcja PNSPCA oparta na sieci (predykcji PNN). Jako zestaw treningowy wybierane są szeregi kolejnych odstepów liczb wstecz od losowania zaznaczonego jako ostatnie. Dla przykładu dla parametru funkcji = 3 bedą to przebiegi:
Działa analogicznie jak funkcja PNNSPC lecz jako kolejne odstępy
są brane odstepy przed wylosowaniem. Np liczba x była wylosowana
w poprzednich okresach po odstępach 6,8, 11
Czyli odpowiedzią będzie 0 odstęp jeżeli po takiej serii była wylosowana
i nastepny odstęp jeżeli po takiej serii nie była losowana.
|
|
•dogóry
|
|



































